2019年AMC 10B试题/第1题
问题
艾丽西亚有两个容器。第一个容器 \( \frac{5}{6} \) 装满了水,第二个容器是空的。她把第一个容器里的水全部倒入第二个容器,此时第二个容器 \( \frac{3}{4} \) 装满了水。求第一个容器的容积与第二个容器的容积之比。
(A) \( \frac{5}{8} \) (B) \( \frac{4}{5} \) (C) \( \frac{7}{8} \) (D) \( \frac{9}{10} \) (E) \( \frac{11}{12} \)
解决方案1
设第一个罐子的容积为 \( A \) ,第二个罐子的容积为 \( B \) 。已知 \( \frac{3}{4}A = \frac{5}{6}B \) 。
我们发现 \( \frac{A}{B} = \frac{\left( \frac{3}{4}\right) }{\left( \frac{5}{6}\right) } = O \) 。(D) \( \frac{9}{10} \) 。
我们已经知道这是较小体积与较大体积之比,因为它小于1。
解决方案 2
另一种解法是给第一个容器设定一个最大容积——假设为72,于是第一个容器实际装有60的体积,第二个容器同样装有60的体积,因此得到 \( {60} \cdot \frac{4}{3} = {80} \) 。所以答案是
\[ \frac{72}{80} = \left( {\text{ D }{.9}\frac{9}{10}}\right) \]
2019年AMC 10B试题/第2题
以下问题同时出现在2019年AMC 10B第2题和2019年AMC 12B第2题,因此两道题均重定向至此页面。
问题
考虑命题“若 \( n \) 不是素数,则 \( n - 2 \) 是素数”。下列哪个 \( n \) 的值是该命题的反例?
(A) 11 (B) 15 (C) 19 (D) 21 (E) 27
解答
由于反例必须是 \( n \) 的值且该值不是素数, \( n \) 必须是合数,因此我们排除 \( \mathrm{A} \) 和 \( \mathrm{C} \) 。接下来,我们将剩余选项减去2,发现只有当 \( n = \) (E) 27时, \( n - 2 \) 才不是素数。
2019 AMC 10B 试题/第3题
题目
某高中共有500名学生,其中 \( {40}\% \) 的高年级学生演奏乐器,而 \( {30}\% \) 的非高年级学生不演奏乐器。总体而言, \( {46.8}\% \) 的学生不演奏乐器。问有多少非高年级学生演奏乐器?(A) 66 (B) 154 (C) 186 (D) 220 (E) 266
解答1
\( {60}\% \) 的高年级学生不演奏乐器。若用 \( x \) 表示高年级学生人数,则
\[ \frac{3}{5}x + \frac{3}{10} \cdot \left( {{500} - x}\right) = \frac{468}{1000} \cdot {500} \]
\[ \frac{3}{5}x + {150} - \frac{3}{10}x = {234} \]
\[ \frac{3}{10}x = {84} \]
\[ x = {84} \cdot \frac{10}{3} = {280} \]
因此共有 \( {500} - x = {220} \) 名非高年级学生。由于 \( {70}\% \) 的非高年级学生演奏乐器, \( {220} \cdot \frac{7}{10} = \) (B) 154 ~IronicNinja
解答2
设 \( x \) 为高年级学生人数, \( y \) 为非高年级学生人数。则
\[ \frac{3}{5}x + \frac{3}{10}y = \frac{468}{1000} \cdot {500} = {234} \]
两边同乘10得
\[ {6x} + {3y} = {2340} \]
同时, \( x + y = {500} \) ,因为全校共有500名学生。
解此方程组得 \( x = {280} \) , \( y = {220} \) 。
由于 \( {70}\% \) 的非高年级学生演奏乐器,答案即为220的 \( {70}\% \) ,得到(B) 154
解答3(利用选项)
我们可明显推断出 \( {70}\% \) 的非高年级学生确实演奏乐器,但由于演奏乐器的总比例为 \( {46.8}\% \) ,非高年级人数相对较少。凭直觉可知答案约为 \( \mathrm{B} \) 或 \( \mathrm{C} \) 。检验这两个选项后得到答案 \( \left( B\right) {154} \) 。参见
2019年AMC 10B试题/第4题
问题
所有满足 \( {ax} + {by} = c \) 且 \( a, b, c \) 构成等差数列的直线都经过同一个点。该点的坐标是什么?
(A)(-1,2) (B)(0,1) (C)(1,-2) (D)(1,0) (E)(1,2)
解决方案 1
如果所有直线都满足条件,那么我们只需为 \( a \) 、 \( b \) 和 \( c \) 代入构成等差数列的值。我们使用 \( a = 1 \) 、 \( b = 2 \) 、 \( c = 3 \) 以及 \( a = 1 \) 、 \( b = 3 \) 、 \( c = 5 \) 。于是得到的两条直线为:
\[ x + {2y} = 3 \]
\[ x + {3y} = 5 \]
使用消元法进行推导
\[ y = 2 \]
并将其代入之前的一条直线方程,我们得到
\[ x + 4 = 3 \Rightarrow x = - 1 \]
因此,公共点为 \( \Delta \) (A)(-1,2)。
~讽刺忍者
解决方案 2
我们知道 \( a \) 、 \( b \) 和 \( c \) 构成一个等差数列,因此若公差为 \( d \) ,则可表示为 \( a, b, c = a, a + d, a + {2d}. \) 。现在我们得到 \( {ax} + \left( {a + d}\right) y = a + {2d} \) ,展开后得到 \( {ax} + {ay} + {dy} = a + {2d} \) 。因式分解得
\( a\left( {x + y - 1}\right) + d\left( {y - 2}\right) = 0 \) 。由于这必须始终成立(无论 \( x \) 和 \( y \) 取何值),我们必须有 \( x + y - 1 = 0 \) 和 \( y - 2 = 0 \) ,因此 \( x, y = - 1,2, \) ,公共点为 \( \left| {\mathbf{\left( A\right) }\left( {-1,2}\right) }\right| \) 。
2019年AMC 10B试题/第5题
问题
三角形 \( {ABC} \) 位于第一象限。点 \( A \) 、 \( B \) 和 \( C \) 分别关于直线 \( y = x \) 对称到点 \( {A}^{\prime } \) 、 \( {B}^{\prime } \) 和 \( {C}^{\prime } \) 。假设三角形的任一顶点都不在直线 \( y = x \) 上。以下哪项陈述并非总是成立?
\( \mathbf{\left( A\right) } \) 三角形 \( {A}^{\prime }{B}^{\prime }{C}^{\prime } \) 位于第一象限。
(B)三角形 \( {ABC} \) 与 \( {A}^{\prime }{B}^{\prime }{C}^{\prime } \) 面积相等。
(C)直线 \( A{A}^{\prime } \) 的斜率为-1。
(D)直线 \( A{A}^{\prime } \) 与 \( C{C}^{\prime } \) 的斜率相同。
(E)直线 \( {AB} \) 与 \( {A}^{\prime }{B}^{\prime } \) 互相垂直。
解答
我们逐一分析所有选项。
\( \mathbf{\left( A\right) } \) :显然 \( \mathbf{\left( A\right) } \) 成立,因为第一象限内的点具有非负的 \( x \) -坐标和 \( y \) -坐标,其交换坐标后的反射点同样具有非负的 \( x \) -坐标和 \( y \) -坐标。
\( \mathbf{\left( B\right) } \) :两三角形面积相等,因为 \( \bigtriangleup {ABC} \) 与 \( \bigtriangleup {A}^{\prime }{B}^{\prime }{C}^{\prime } \) 为同一三角形(全等)。更正式地说,面积在反射下保持不变。
\( \mathbf{\left( C\right) } \) :若点 \( A \) 的坐标为(p, q),则 \( {A}^{\prime } \) 的坐标为(q, p)。因此斜率为 \( \frac{p - q}{q - p} = - 1 \) ,故该命题成立。(题目
已说明点 \( A \) 、 \( B \) 、 \( C \) 均不在直线 \( y = x \) 上,故不存在除零风险)。
(D):重复(C)的论证可知,两直线斜率均为-1,因此该命题亦成立。
\( \mathbf{\left( E\right) } \) :通过排除法,这必然是答案。事实上,若点 \( A \) 的坐标为(p, q),点 \( B \) 的坐标为(r, s),则 \( {A}^{\prime } \) 与 \( {B}^{\prime } \) 的坐标分别为(q, p)与(s, r)。直线 \( {AB} \) 与 \( {A}^{\prime }{B}^{\prime } \) 的斜率乘积为 \( \frac{s - q}{r - p} \cdot \frac{r - p}{s - q} = 1 \neq - 1 \) ,故这些直线从不互相垂直(利用垂直的“负倒数”条件)。
因此答案为 \( \sigma \) (E)
反例
若 \( \left( {{x}_{1},{y}_{1}}\right) = \left( {2,3}\right) \) 且 \( \left( {{x}_{2},{y}_{2}}\right) = \left( {7,1}\right) \) ,则 \( {AB} \) 的斜率 \( {m}_{AB} \) 为 \( \frac{1 - 3}{7 - 2} = - \frac{2}{5} \) ,而 \( {A}^{\prime }{B}^{\prime },{m}_{{A}^{\prime }{B}^{\prime }} \) 的斜率为 \( \frac{7 - 2}{1 - 3} = - \frac{5}{2} \) 。 \( {m}_{{A}^{\prime }{B}^{\prime }} \) 是 \( {m}_{AB} \) 的倒数,但不是 \( {m}_{AB} \) 的负倒数。为推广起见,设 \( \left( {{x}_{1},{y}_{1}}\right) \) 表示点 \( A \) 的坐标, \( \left( {{x}_{2},{y}_{2}}\right) \) 表示点 \( B \) 的坐标, \( {m}_{AB} \) 表示线段 \( {AB} \) 的斜率, \( {m}_{{A}^{\prime }{B}^{\prime }} \) 表示线段 \( \overline{{A}^{\prime }{B}^{\prime }} \) 的斜率。则 \( {A}^{\prime } \) 的坐标为 \( \left( {{y}_{1},{x}_{1}}\right) \) , \( {B}^{\prime } \) 的坐标为 \( \left( {{y}_{2},{x}_{2}}\right) \) 。于是 \( {m}_{AB} = \frac{{y}_{2} - {y}_{1}}{{x}_{2} - {x}_{1}} \) ,且 \( {m}_{{A}^{\prime }{B}^{\prime }} = \frac{{x}_{2} - {x}_{1}}{{y}_{2} - {y}_{1}} = \frac{1}{{m}_{ab}} \) 。若 \( {y}_{1} \neq {y}_{2} \) 且 \( {x}_{1} \neq {x}_{2},\frac{1}{{m}_{AB}} \neq \frac{1}{{m}_{{A}^{\prime }{B}^{\prime }}} \Rightarrow {m}_{AB} \neq {m}_{{A}^{\prime }{B}^{\prime }} \) ,则在这些情况下条件不成立。
2019 AMC 10B 试题/第6题
以下题目同时出现在2019 AMC 10B第6题和2019 AMC 12B第4题,因此两题均重定向至此页面。
题目
存在一个正整数 \( n \) ,使得 \( \left( {n + 1}\right) ! + \left( {n + 2}\right) ! = n! \cdot {440} \) 。 \( n \) 的各位数字之和是多少?
(A) 3 (B) 8 (C) 10 (D) 11 (E) 12
解法1
\[ \left( {n + 1}\right) n! + \left( {n + 2}\right) \left( {n + 1}\right) n! = {440} \cdot n! \]
\[ \Rightarrow n!\left\lbrack {n + 1 + \left( {n + 2}\right) \left( {n + 1}\right) }\right\rbrack = {440} \cdot n! \]
\[ \Rightarrow n + 1 + {n}^{2} + {3n} + 2 = {440} \]
\[ \Rightarrow {n}^{2} + {4n} - {437} = 0 \]
使用二次公式求解,
\( n = \frac{-4 \pm \sqrt{{16} + {437} \cdot 4}}{2} = \frac{-4 \pm {42}}{2} = \frac{38}{2} = {19} \) (因为显然 \( n \geq 0 \) )。
因此答案为 \( 1 + 9 = \) (C) 10
解法2
两边同除以 \( n! \) 得
\[ \left( {n + 1}\right) + \left( {n + 2}\right) \left( {n + 1}\right) = {440} \Rightarrow {n}^{2} + {4n} - {437} = 0 \Rightarrow \left( {n - {19}}\right) \left( {n + {23}}\right) = 0 \]
由于 \( n \) 非负, \( n = {19} \) 。答案为 \( 1 + 9 = \) (C)10
解法3
两边同除以 \( n! \) ,如前所述,得到 \( \left( {n + 1}\right) + \left( {n + 1}\right) \left( {n + 2}\right) = {440} \) 。现在提取公因式 \( \left( {n + 1}\right) \) ,得到 \( \left( {n + 1}\right) \left( {n + 3}\right) = {440} \) 。考虑440的质因数分解,稍作尝试可得 \( n + 1 = {20} \) 与 \( n + 3 = {22} \) ,于是 \( n = {19} \) ,故答案为 \( 1 + 9 = \) (C) 10。
2019 AMC 10B 试题/第7题
题目
商店里每颗糖果的价格都是整数美分。Casper的钱恰好够买12颗红色糖果、14颗绿色糖果、15颗蓝色糖果,或 \( n \) 颗紫色糖果。已知一颗紫色糖果售价20美分,求 \( n \) 的最小可能值。
(A) 18 (B) 21 (C) 24 (D) 25 (E) 28
解法1
若他拥有的钱恰好够买12颗红色糖果、14颗绿色糖果和15颗蓝色糖果,则他最少拥有的钱为 \( \mathrm{{lcm}}\left( {{12},{14},{15}}\right) = {420} \) 美分。由于一颗紫色糖果售价20美分, \( n \) 的最小可能值为 \( \frac{420}{20} = \) (B) 21 ~IronicNinja
解法2
我们只需找到一个能被12、14和15整除的 \( {20n} \) 值。注意到 \( {20} \cdot {18} \) 能被12和15整除,但不能被14整除; \( {20} \cdot {21} \) 能被12、14和15整除,这意味着我们恰好有420美分,可购买任意一种糖果,因此 \( n \) 的最小值为 \( \left| {\mathbf{\left( B\right) }{21}}\right| \) 。
解法3
我们可观察到,紫色糖果数量乘以20必须能被7整除(因为有14颗绿色糖果),也必须能被3整除(因为有12颗红色糖果)。 \( 7 * 3 = {21} \) ,故答案为 \( \alpha \) 。21。
2019 AMC 10B 试题/第8题
题目
下图所示为一个正方形和四个等边三角形,每个三角形的一条边落在正方形的一条边上,且每个三角形的边长为2,四个三角形的第三个顶点均汇聚于正方形中心。正方形内部、三角形外部的区域被阴影覆盖。求阴影区域的面积。
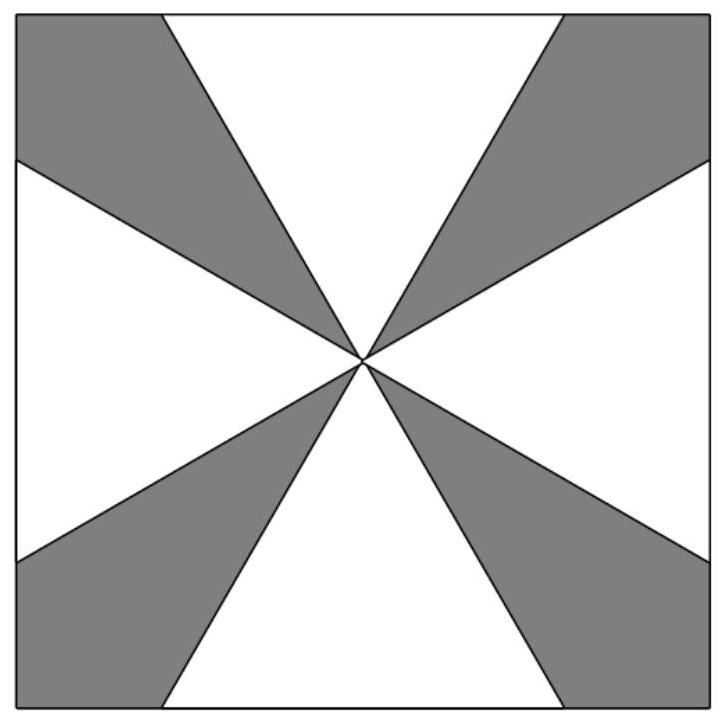
(B) \( {12} - 4\sqrt{3} \) (C) \( 3\sqrt{3} \) (D) \( 4\sqrt{3} \) (E) \( {16} - 4\sqrt{3} \) 解法1
我们注意到,正方形可被分割成4个全等的小正方形,等边三角形的高即为该小正方形的边长。因此,每个位于小正方形内的阴影部分面积等于小正方形面积减去已平分的三角形面积。#storm
当我们将一个等边三角形(equilateral triangle)平分时,会得到两个 \( {30}^{ \circ } - {60}^{ \circ } - {90}^{ \circ } \) 三角形。
因此,高(altitude)同时也是其中一个小正方形的边长,为 \( \sqrt{3} \) 。接着我们可以计算这两个三角形的面积为 \( 2 \cdot \frac{1 \cdot \sqrt{3}}{2} = \sqrt{3} \) 。
每个小正方形的面积等于其边长的平方,即 \( {\left( \sqrt{3}\right) }^{2} = 3 \) 。
因此,每个正方形中阴影区域的面积为 \( 3 - \sqrt{3} \) 。
由于共有4个这样的正方形,我们将该面积乘以4,得到
\( 4\left( {3 - \sqrt{3}}\right) = \) (B) \( {12} - 4\sqrt{3} \) 作为答案。
解法2
通过考虑等边三角形的高(如解法1所示),可知正方形的边长为 \( 2\sqrt{3} \) 。根据勾股定理(Pythagorean Theorem),正方形的对角线长为 \( \sqrt{{12} + {12}} = \sqrt{24} = 2\sqrt{6} \) 。因此,四个阴影风筝形之一的高为 \( \sqrt{6} \) 。接下来,我们只需求出该风筝形的长度。再次使用勾股定理,该长度为 \( \frac{2\sqrt{3} - 2}{2} \times \sqrt{2} = \sqrt{3} - 1 = \sqrt{6} - \sqrt{2} \) 。利用面积=长×宽,一个风筝形的面积为 。
。
2019 AMC 10B 试题/第9题
题目
函数 \( f \) 定义为
\[ f\left( x\right) = \lfloor \left| x\right| \rfloor - \left| {\lfloor x\rfloor }\right| \]
对所有实数 \( x \) ,其中 \( \lfloor r\rfloor \) 表示小于或等于实数 \( r \) 的最大整数。 \( f \) 的值域是什么?
(A) \( \{ - 1,0\} \;\left( \text{B}\right) \) 非正整数集合 (C) \( \{ - 1,0,1\} \) (D) \( \{ 0\} \) (E) \( \mathrm{T} \)
解法1
我们需要考虑以下四种情况。
情况1: \( x \) 为正整数。不失一般性,设 \( x = 1 \) 。则 \( f\left( 1\right) = 1 - 1 = 0 \) 。
情况2: \( x \) 为正分数。不失一般性,设 \( x = \frac{1}{2} \) 。则 \( f\left( \frac{1}{2}\right) = 0 - 0 = 0 \) 。
情况3: \( x \) 为负整数。不失一般性,设 \( x = - 1 \) 。则 \( f\left( {-1}\right) = 1 - 1 = 0 \) 。
情况4: \( x \) 为负分数。不失一般性,设 \( x = - \frac{1}{2} \) 。则 \( f\left( {-\frac{1}{2}}\right) = 0 - 1 = - 1 \) 。
因此函数 \( f \) 的值域为 \( \left( \mathbf{A}\right) \{ - 1,0\} \)
-lronicNinja,由别人编辑,嘿嘿
解法2
容易验证,当 \( x \) 为整数时, \( f\left( x\right) \) 为零。因此只需考虑 \( x \) 不是整数的情况。
当 \( x \) 为正数时, \( \lfloor x\rfloor \geq 0 \) ,所以
\[ f\left( x\right) = \lfloor \left| x\right| \rfloor - \left| {\lfloor x\rfloor }\right| \]
\[ = \lfloor x\rfloor - \lfloor x\rfloor \]
\[ = 0 \]
当 \( x \) 为负数时,设 \( x = - a - b \) 由整数部分 \( a \) 和小数部分 \( b \) 组成(两者均 \( \geq 0 \) ):
\[ f\left( x\right) = \lfloor \left| {-a - b}\right| \rfloor - \left| {\lfloor - a - b\rfloor }\right| \]
\[ = \left\lfloor {a + b}\right\rfloor - \left| {-a - 1}\right| \]
\[ = a - \left( {a + 1}\right) = - 1 \]
因此, \( f \) 的值域为 \( \left( \mathbf{A}\right) \{ - 1,0\} \)
注:对于 \( x \) 为负非整数的情况,也可按如下方式求解:
2019 AMC 10B 试题/第10题
题目
在某一平面内,点 \( A \) 与 \( B \) 相距10个单位。问该平面内有多少个点 \( C \) ,使得三角形 \( \bigtriangleup {ABC} \) 的周长为50个单位且面积为100平方单位?
(A) 0 (B) 2 (C) 4 (D) 8 (E) 无穷多个
解法1
注意到无论我们选哪个点作为 \( C \) , \( {AB} \) 都将是三角形的底边。不失一般性,设点 \( A \) 和 \( B \) 分别为(0,0)和(0,10),因为对于其他任意两点,我们都可以通过旋转平面,使它们在新坐标系下变为(0,0)和(0,10)。当我们选取点 \( C \) 时,必须确保其 \( y \) 坐标为 \( \pm {20} \) ,因为这是三角形面积等于100的唯一可能。
当周长最小时,由对称性,我们将 \( C \) 置于中点(5,20)。易见 \( {AC} \) 和 \( {BC} \) 均等于 \( \sqrt{{20}^{2} + {5}^{2}} = \sqrt{425} \) 。该最小三角形的周长为 \( 2\sqrt{425} + {10} \) ,大于50。由于最小周长已超过50,不存在满足条件的三角形,因此答案为 \( \left( \mathbf{A}\right) 0 \) 。
~IronicNinja
解法2
不失一般性,设 \( {AB} \) 为一条水平线段,长度为10。现在意识到 \( C \) 必须位于与 \( {AB} \) 平行且垂直距离为20的某条直线上。但 \( {10} + {20} + {20} \) 已经是50,这无法构成三角形。否则,不失一般性, \( {AC} < {20} \) 。作高 \( {CD} \) ,我们得到一个直角三角形 \( {ACD} \) ,其斜边为 \( {AC} < {20} \) ,一条直角边为 \( {CD} = {20} \) ,这显然不可能,再次得到答案为(A,0)。
解法3
面积=100,周长=50,半周长 \( s = {50}/2 = {25} \) , \( z = {AB} = {10} \) , \( x = {AC} \) 和 \( y = {50} - {10} - x = {40} - x \) 。
使用以半周长 \( s \) 及边长 \( x \) 、 \( y \) 和 \( z \) 表示的三角形面积通用公式,面积=
\[ \sqrt{\left( s\right) \left( {s - x}\right) \left( {s - y}\right) \left( {s - z}\right) }\text{. (Heron's formula)} \]
\[ {100} = \sqrt{({25})({25} - {10})({25} - x)({25} - ({40} - x))} = \sqrt{({375})({25} - x)(x - {15})} \]
两边平方,除以375并展开多项式,得到 \( {35x} - {x}^{2} - {375} = {80}/3 \) 。
\( {x}^{2} - {35x} + \left( {{375} + {80}/3}\right) = 0 \) 且判别式为
\( \left( {{\left( -{35}\right) }^{2} - 4 * 1 * {401}.\overline{6}}\right) < 0 \) ,因此无实数解。
2019 AMC 10B 试题/第11题
题目
两个罐子中各有相同数量的弹珠,每颗弹珠要么是蓝色要么是绿色。在罐1中,蓝色与绿色弹珠的比例为 \( 9 : 1 \) ,罐2中蓝色与绿色弹珠的比例为 \( 8 : 1 \) 。所有绿色弹珠共有95颗。罐1比罐2多多少颗蓝色弹珠?
(A) 5 (B) 10 (C) 25 (D) 45 (E) 50
解法
设每个罐子的弹珠数量为 \( x \) (因为题目说明它们数量相同)。于是 \( \frac{x}{10} \) 是罐1中的绿色弹珠数, \( \frac{x}{9} \) 是罐2中的绿色弹珠数。由于 \( \frac{x}{9} + \frac{x}{10} = \frac{19x}{90} \) ,我们有 \( \frac{19x}{90} = {95} \) ,因此每个罐子有 \( x = {450} \) 颗弹珠。因为 \( \frac{9x}{10} \) 是罐1中的蓝色弹珠数, \( \frac{8x}{9} \) 是罐2中的蓝色弹珠数,所以罐1比罐2多 \( \frac{9x}{10} - \frac{8x}{9} = \frac{x}{90} = 5 \) 颗弹珠。这意味着答案是 \( \left| {\left( \mathbf{A}\right) 5}\right| \) 。
2019 AMC 10B 试题/第12题
题目
小于2019的正整数在七进制表示中,其各位数字之和的最大可能值是多少?
(A) 11 (B) 14 (C) 22 (D) 23 (E) 27
解法1
注意到 \( {2019}_{10} = {5613}_{7} \) 。为了使各位数字之和最大,我们希望尽可能多地出现6(因为6是七进制中的最大数字),这将在以下两个数中实现:或。因此,答案是
\( 4 + 6 + 6 + 6 = 5 + 5 + 6 + 6 = 6 \)
~IronicNinja把这套卷子做了100遍
解法2
注意,所有5位及以上的七进制数实际上都大于2019。由于使用4位数能得到的第一个答案是,我们从最小的、各位数字之和为的七进制数开始,即。但这大于,于是我们继续尝试,它小于2019。所以
答案是
2019 AMC 10B 第13题
题目
对于哪些实数 \( x \) ,数4,6,8,17和 \( x \) 的中位数等于这五个数的平均数?求所有这些实数 \( x \) 的和。
(A) -5 (B) 0 (C) 5 (D) \( \frac{15}{4} \) (E) \( \frac{35}{4} \)
解答
平均数为 \( \frac{4 + 6 + 8 + {17} + x}{5} = \frac{{35} + x}{5} \) 。
中位数有三种可能:6、8或 \( x \) 。
先从6开始讨论。
\( \frac{{35} + x}{5} = 6 \) 有解 \( x = - 5 \) ,且该序列为-5,4,6,8,17,
其中位数确实为6,因此这是一个有效解。
现在设中位数为8。
\( \frac{{35} + x}{5} = 8 \) 得到 \( x = 5 \) ,因此序列为 4,5,6,8,17,其中位数
6,因此这是无效的。
最后,我们将中位数设为 \( x \) 。
\[ \frac{{35} + x}{5} = x \Longrightarrow {35} + x = {5x} \Longrightarrow x = \frac{35}{4} = {8.75}\text{, and the} \]
序列为4,6,8,8.75,17,其中位数为8。因此,该情况再次无效。
因此 \( x \) 的唯一可能取值为0:
2019年AMC 10B试题/第14题
问题
\( {19}! \) 的十进制(base-ten)表示为 \( {121},{6T5},{100},{40M},{832},{H00} \) ,其中 \( T \) 、 \( M \) 和 \( H \) 表示未给出的数字。那么 \( T + M + H \) 是多少?
(A) 3 (B) 8 (C) 12 (D) 14 (E) 17
解决方案1
我们可以通过注意到 \( {19}! \) 末尾有3个0来求出 \( H = 0 \) ,因为其质因数分解中有三个5。接下来,我们利用 \( {19}! \) 同时是11和9的倍数这一事实。它们的整除规则(见解法2)告诉我们
\( T + M \equiv 3{\;(\operatorname{mod}\;9)} \) ,并且 \( T - M \equiv 7{\;(\operatorname{mod}\;{11})} \) 。通过猜测与验证,我们发现 \( T = 4, M = 8 \) 是一个有效解。因此答案为 \( 4 + 8 + 0 = 0 \)
解法2(与解法1类似)
我们知道 \( H = 0 \) ,因为 \( {19}! \) 以三个零结尾(见解法1)。此外,我们知道9和11都是 \( {19}! \) 的因数。我们可以直接利用9和11的整除规则来求 \( T \) 和 \( M \) 。要使 \( {19}! \) 能被9整除,其各位数字之和必须能被9整除。将各位数字相加,我们得到 \( T + M + {33} \) 必须能被9整除。这样答案只能是 \( \mathrm{A} \) 或 \( \mathrm{C} \) 。现在我们检验能否被11整除。一个数能被11整除的条件是其交替和必须能被11整除(例如,对于数2728, \( 2 - 7 + 2 - 8 = - {11} \) ,所以2728能被11整除)。应用交替
和检验到本题,我们看到 \( T - M - 7 \) 必须能被11整除。通过观察,我们发现当 \( T = 4 \) 且 \( M = 8 \) 时成立。其和为 \( 8 + 4 + 0 = \left( \begin{array}{l} \mathbf{C} \end{array}\right) {12}. \)
2019 AMC 10B 试题/第15题
题目
直角三角形 \( {T}_{1} \) 和 \( {T}_{2} \) 的面积分别为1和2。 \( {T}_{1} \) 的一条边与 \( {T}_{2} \) 的一条边全等, \( {T}_{1} \) 的另一条边又与 \( {T}_{2} \) 的另一条边全等。求 \( {T}_{1} \) 和 \( {T}_{2} \) 的第三边长度之积的平方。
(A) \( \frac{28}{3} \) (B) 10 (C) \( \frac{32}{3} \) (D) \( \frac{34}{3} \) (E) 12
解法1
首先,设这两条全等的边分别为 \( x \) 和 \( y \) ,其中 \( y > x \) 。满足题设条件的唯一情形是: \( x \) 既是 \( {T}_{2} \) 的较短直角边,又是 \( {T}_{1} \) 的较长直角边;而 \( y \) 既是 \( {T}_{2} \) 的较长直角边,又是 \( {T}_{1} \) 的斜边。
注意,这意味着我们要求的值就是
\( \sqrt{{x}^{2} + {y}^{2}} \cdot \sqrt{{y}^{2} - {x}^{2}} = \sqrt{{y}^{4} - {x}^{4}} \) 的平方,即 \( {y}^{4} - {x}^{4} \) 。
面积条件给出两个方程: \( \frac{xy}{2} = 2 \) 和 \( \frac{x\sqrt{{y}^{2} - {x}^{2}}}{2} = 1 \) 。
这意味着 \( y = \frac{4}{x} \) 且 \( \frac{4}{{x}^{2}} = {y}^{2} - {x}^{2} \) 。
由第二个方程得 \( {x}^{2}{y}^{2} - {x}^{4} = 4 \) ,因此由于 \( {xy} = 4 \) , \( {x}^{4} = {12} \) 。
因为 \( y = \frac{4}{x} \) ,我们得到 \( {y}^{4} = \frac{256}{12} = \frac{64}{3} \) 。
我们要求的值就是 \( {y}^{4} - {x}^{4} = \frac{{64} - {36}}{3} = \frac{28}{3} \) ,所以答案是 \( \left( \mathbf{A}\right) \frac{28}{3} \)
解法2
与解法1相同,我们有 \( \frac{xy}{2} = 2 \) 和 \( \frac{x\sqrt{{y}^{2} - {x}^{2}}}{2} = 1 \) 。
将两个方程两边平方得到 \( {x}^{2}{y}^{2} = {16} \) 和 \( {x}^{2}\left( {{y}^{2} - {x}^{2}}\right) = 4 \) 。
\[ \text{Let}a = {x}^{2}\text{and}b = {y}^{2}\text{. Then}b = \frac{16}{a}\text{, and} \]
\[ a\left( {\frac{16}{a} - a}\right) = 4 \Rightarrow {16} - {a}^{2} = 4 \Rightarrow a = 2\sqrt{3}\text{, so}b = \frac{16}{2\sqrt{3}} = \frac{8\sqrt{3}}{3}\text{.} \]
我们要求 \( {y}^{4} - {x}^{4} = {b}^{2} - {a}^{2} \) 的值,因此答案是 \( \frac{64}{3} - {12} = \) (A) \( \frac{28}{3} \)
解法3
首先,设这两个直角三角形为 \( \bigtriangleup {ABC} \) 和 \( \bigtriangleup {EDF} \) ,其中 \( \bigtriangleup {ABC} \) 是较小的三角形。与解法1相同,设 \( \overline{AB} = \overline{EF} = x \) 和 \( \overline{BC} = \overline{DF} = y \) 。此外,设 \( \overline{AC} = z \) 和 \( \overline{DE} = w \)
已知 \( \left\lbrack {ABC}\right\rbrack = 1 \) 和 \( \left\lbrack {EDF}\right\rbrack = 2 \) ,因此利用 \( \operatorname{area} = \frac{bh}{2} \) ,我们有 \( \frac{xy}{2} = 1 \) 和 \( \frac{xw}{2} = 2 \) 。将两式相除,得到 \( \frac{xy}{xw} = \frac{y}{w} = 2 \) ,于是 \( y = {2w} \) 。
因此 \( \bigtriangleup {EDF} \) 是一个 \( {30}^{ \circ } - {60}^{ \circ } - {90}^{ \circ } \) 直角三角形,这意味着 \( x = w\sqrt{3} \) 。现在在 \( \bigtriangleup {ABC} \) 中应用勾股定理,
\[ {\left( w\sqrt{3}\right) }^{2} + {\left( 2w\right) }^{2} = {z}^{2} \Rightarrow 3{w}^{2} + 4{w}^{2} = {z}^{2} \Rightarrow 7{w}^{2} = {z}^{2} \Rightarrow w\sqrt{7} = z. \]
题目要求每个三角形第三边长度之积的平方,即 \( {\left( wz\right) }^{2} \) 。
通过代入,我们发现 \( {wz} \) = \( \left( w\right) \left( {w\sqrt{7}}\right) = {w}^{2}\sqrt{7} \) 。我们还知道
\[ \frac{xw}{2} = 1 \Rightarrow \frac{\left( w\right) \left( {w\sqrt{3}}\right) }{2} = 1 \Rightarrow \left( w\right) \left( {w\sqrt{3}}\right) = 2 \Rightarrow {w}^{2}\sqrt{3} = 2 \Rightarrow {w}^{2} = \frac{2\sqrt{3}}{3} \]
由于我们要求 \( {\left( {w}^{2}\sqrt{7}\right) }^{2} \) ,两边同乘以 \( \sqrt{7} \) 得到 \( {w}^{2}\sqrt{7} = \frac{2\sqrt{21}}{3} \) 。现在平方
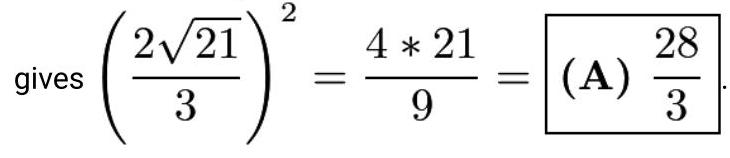
2019 AMC 10B 试题/第16题
题目
在 \( \bigtriangleup {ABC} \) 中, \( C \) 处为直角,点 \( D \) 位于 \( \overline{AB} \) 内部,点 \( E \) 位于 \( \overline{BC} \) 内部,使得 \( {AC} = {CD},{DE} = {EB}, \) 且比例 \( {AC} : {DE} = 4 : 3 \) 。求比例 \( {AD} : {DB} \) ?
(A) \( 2 : 3 \) (B) \( 2 : \sqrt{5} \) (C) \( 1 : 1 \) (D) \( 3 : \sqrt{5} \) (E) \( 3 : 2 \)
解法1
不失一般性,设 \( {AC} = {CD} = 4 \) 和 \( {DE} = {EB} = 3 \) 。设 \( \angle A = \alpha \) 和 \( \angle B = \beta = {90}^{ \circ } - \alpha \) 。由于 \( \bigtriangleup {ACD} \) 和 \( \bigtriangleup {DEB} \) 为等腰三角形, \( \angle {ADC} = \alpha \) 和 \( \angle {BDE} = \beta \) 。于是 \( \angle {CDE} = {180}^{ \circ } - \alpha - \beta = {90}^{ \circ } \) ,因此 \( \bigtriangleup {CDE} \) 是一个 \( 3 - 4 - 5 \) 三角形,且 \( {CE} = 5 \) 。
于是 \( {CB} = 5 + 3 = 8 \) ,且 \( \bigtriangleup {ABC} \) 是一个 \( 1 - 2 - \sqrt{5} \) 三角形。
在等腰三角形 \( \bigtriangleup {ACD} \) 和 \( \bigtriangleup {DEB} \) 中,从 \( C \) 和 \( E \) 分别向 \( {AB} \) 作垂线;记垂足分别为 \( {P}_{C} \) 和 \( {P}_{E} \) 。于是由AAA相似得 \( \bigtriangleup {AC}{P}_{C} \sim \bigtriangleup {ABC} \) ,从而 \( A{P}_{C} = {P}_{C}D = \frac{4}{\sqrt{5}} \) ,且 \( {AD} = 2 \times \frac{4}{\sqrt{5}} \) 。同理可得 \( {BD} = 2 \times \frac{6}{\sqrt{5}} \) 和 \( {AD} : {DB} = \left( \text{A}\right) 2 : 3 \) 。
解法2
设 \( {AC} = {CD} = {4x} \) ,且 \( {DE} = {EB} = {3x} \) 。(在本解法中, \( A \) 位于 \( C \) 上方, \( B \) 位于 \( C \) 右侧)。再设 \( \angle A = {t}^{ \circ } \) ,于是 \( \angle {ACD} = {\left( {180} - 2t\right) }^{ \circ } \) ,这意味着 \( \angle {DCB} = {\left( 2t - {90}\right) }^{ \circ } \) 。同理, \( \angle B = {\left( {90} - t\right) }^{ \circ } \) ,这意味着 \( \angle {BED} = 2{t}^{ \circ } \) 。进而可得 \( \angle {DEC} = {\left( {180} - 2t\right) }^{ \circ } \) 。
现在我们发现
\( {\angle CDE} = {180}^{ \circ } - {\angle ECD} - {\angle DEC} = {180}^{ \circ } - 2{t}^{ \circ } + {90}^{ \circ } - {180}^{ \circ } + 2{t}^{ \circ } = {90}^{ \circ } \) 。因此 \( \bigtriangleup {CDE} \) 是一个直角三角形,其边长分别为 \( {3x} \) 、 \( {4x} \) 和 \( {5x} \) (由勾股定理,或直接用勾股数 \( 3 - 4 - 5 \) )。于是 \( {AC} = {4x} \) (由定义),
\( {BC} = {5x} + {3x} = {8x} \) ,且 \( {AB} = 4\sqrt{5}x \) 。因此 \( \cos \left( {2{t}^{ \circ }}\right) = 2{\cos }^{2}{t}^{ \circ } - 1 \) (由倍角公式),从而 \( 2{\left( \frac{1}{\sqrt{5}}\right) }^{2} - 1 = - \frac{3}{5} \) 。
根据余弦定理(Law of Cosines),在 \( \bigtriangleup {BED} \) 中,若 \( {BD} = d \) ,则有
\[ {d}^{2} = {\left( 3x\right) }^{2} + {\left( 3x\right) }^{2} - 2 \cdot \frac{-3}{5}\left( {3x}\right) \left( {3x}\right) \]
\[ \Rightarrow {d}^{2} = {18}{x}^{2} + \frac{{54}{x}^{2}}{5} = \frac{{144}{x}^{2}}{5} \]
\[ \Rightarrow d = \frac{12x}{\sqrt{5}} \]
现在 \( {AD} = {AB} - {BD} = {4x}\sqrt{5} - \frac{12x}{\sqrt{5}} = \frac{8x}{\sqrt{5}} \) 。因此答案为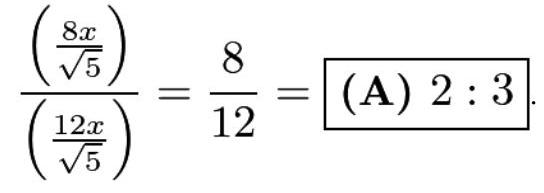
2019 AMC 12B 试题/第13题
题目
一个红球和一个绿球被随机且独立地投入编号为正整数的箱子中,使得对于每个球,其被投入编号为 \( k \) 的箱子的概率为 \( {2}^{-k} \) ,其中 \( k = 1,2,3... \) 。求红球被投入编号比绿球更高的箱子的概率。
(A) \( \frac{1}{4} \) (B) \( \frac{2}{7} \) (C) \( \frac{1}{3} \) (D) \( \frac{3}{8} \) (E) \( \frac{3}{7} \)
解法1
由对称性,红球落入编号更高箱子的概率与绿球落入编号更高箱子的概率相同。显然,两球落入同一箱子的概率为 \( \mathop{\sum }\limits_{{k = 1}}^{\infty }{2}^{-k} \cdot {2}^{-k} = \mathop{\sum }\limits_{{k = 1}}^{\infty }{2}^{-{2k}} = \frac{1}{3} \) (由几何级数求和公式)。因此,由于其余两个概率相等,它们必为 \( \frac{1 - \frac{1}{3}}{2} = 1 \) (C) \( \frac{1}{3} \) 。
解法2
假设绿球落入编号为 \( i \) 的箱子,其中 \( i \geq 1 \) 。此事件发生的概率为 \( \frac{1}{{2}^{i}} \) 。在此条件下,红球落入编号更高箱子的概率为 \( \frac{1}{{2}^{i + 1}} + \frac{1}{{2}^{i + 2}} + \ldots = \frac{1}{{2}^{i}} \) (由几何级数求和公式)。因此,绿球落入编号 \( i \) 且红球落入编号大于 \( i \) 的箱子的概率为 \( {\left( \frac{1}{{2}^{i}}\right) }^{2} = \frac{1}{{4}^{i}} \) 。从 \( i = 1 \) 到无穷求和,我们得到
\[ \mathop{\sum }\limits_{{i = 1}}^{\infty }\frac{1}{{4}^{i}} = 1 \]
其中我们再次使用了几何级数求和公式。(或者,若此和等于 \( n \) ,则通过写出各项并两边同乘4,可得 \( {4n} = n + 1 \) ,从而 \( n = \frac{1}{3} \) 。)
解法3
红球在编号 \( k,\Pr \left( \text{Green Below Red}\right) = \mathop{\sum }\limits_{{i = 1}}^{{k - 1}}{2}^{-i} \) (GBR)且
\( \Pr ( \) 红球在 \( \mathrm{{Bin}}\mathrm{k} = {2}^{-k} \) (RB)。
\[ \Pr \left( {\mathrm{{GBR}} \mid \mathrm{{RB}}}\right) = \mathop{\sum }\limits_{{k = 1}}^{\infty }{2}^{-k}\mathop{\sum }\limits_{{i = 1}}^{{k - 1}}{2}^{-i} = \mathop{\sum }\limits_{{k = 1}}^{\infty }{2}^{-k} \cdot \frac{1}{2}\left( \frac{1 - {\left( 1/2\right) }^{k - 1}}{1 - 1/2}\right) \]
\[ \mathop{\sum }\limits_{{k = 1}}^{\infty }\frac{1}{{2}^{-k}} - 2\mathop{\sum }\limits_{{k = 1}}^{\infty }\frac{1}{{\left( {2}^{2}\right) }^{-k}} \Rightarrow 1 - 2/3 = D\underline{D\frac{1}{3}} \]
解法4 两球落入相邻编号的箱子的概率为
\[ \frac{1}{2 \times 4} + \frac{1}{4 \times 8} + \frac{1}{8 \times {16}} + \ldots = \frac{1}{8} + \frac{1}{32} + \frac{1}{128} + \cdots = \frac{1}{6}\text{by} \]
几何级数求和公式。类似地,两球落入编号相差2的箱子的概率为
\[ \frac{1}{2 \times 8} + \frac{1}{4 \times {16}} + \frac{1}{8 \times {32}} + \cdots = \frac{1}{16} + \frac{1}{64} + \frac{1}{256} + \cdots = \frac{1}{12} \]
(再次识别出几何级数)。我们可以看到,每在两个球之间增加一个箱子,概率就减半。因此,我们的答案是
\[ \frac{1}{6} + \frac{1}{12} + \frac{1}{24} + \cdots \text{, which, by the geometric series sum formula, is}\left| {\mathbf{C})\frac{1}{3}}\right| \text{.} \]
解法5(快速,概念性)
定义“获胜”为球出现在编号更高的箱子中。
从第一个箱子开始。
该箱子有4种可能结果:红球、绿球、红球和绿球,或空,每种概率均为 \( \frac{1}{4} \) 。若第一个箱子没有球,游戏在第二个箱子重新开始,概率分布相同,因此若
解法6
将无穷几何级数写为 \( \frac{1}{2},\frac{1}{4},\frac{1}{8},\frac{1}{16},\cdots \) 。为求红球落入比绿球编号更高的箱子的概率,只需去掉所有奇数项(即第1、3…项),再求剩余项之和——这实际上与解法2的方法完全等价。写成另一无穷几何序列,剩下 \( \frac{1}{4},\frac{1}{16},\frac{1}{64},\cdots \) 。求和得
\[ \mathop{\sum }\limits_{{i = 1}}^{\infty }\frac{1}{{4}^{i}} = 1 \]
解法7
这立刻像几何级数问题,因此固定绿球落入箱子1,红球落入更高箱子的概率为 \( \frac{1}{2}\left( {\frac{1}{{2}^{2}} + \frac{1}{{2}^{3}} + \ldots }\right) \) ;固定绿球落入箱子2,概率为 \( \frac{1}{{2}^{2}}(\frac{1}{{2}^{3}} + \frac{1}{{2}^{4}} + ...). \) 。将每个概率首项分母提出得 \( \frac{1}{{2}^{3}}\left( {1 + \frac{1}{2} + \frac{1}{{2}^{2}} + ..}\right) + \frac{1}{{2}^{5}}\left( {1 + \frac{1}{2} + \frac{1}{{2}^{2}} + \ldots }\right) + \ldots \) ,于是提出 \( \left( {1 + \frac{1}{2} + \frac{1}{{2}^{2}} + \frac{1}{{2}^{3}} + \ldots }\right) \) 后概率简化为 \( \left( {\frac{1}{{2}^{3}} + \frac{1}{{2}^{5}} + \frac{1}{{2}^{7}} + \ldots }\right) \left( {1 + \frac{1}{2} + \frac{1}{{2}^{2}} + \frac{1}{{2}^{3}} + \ldots }\right) \) ,并使用
公式 \( \frac{a}{1 - r} \) 求两个级数,得 \( \left( \frac{\frac{1}{{2}^{3}}}{1 - \frac{1}{4}}\right) \left( \frac{1}{1 - \frac{1}{2}}\right) \) ,化简为 \( \left\lbrack {\mathbf{C})\frac{1}{3}}\right\rbrack - \) OGBooger
2019 AMC 10B 试题/第18题
题目
一天早晨,亨利决定锻炼,他从家出发,走了 \( \frac{3}{4} \) 的路程前往健身房。健身房距离他家2公里。走到那里后,他改变主意,从当前位置往回走了 \( \frac{3}{4} \) 的路程。到达该点后,他再次改变主意,从那里又向健身房方向走了 \( \frac{3}{4} \) 的距离。如果亨利每次在从上次改变主意的地方向健身房或家方向走了 \( \frac{3}{4} \) 的距离时就改变主意,他将非常接近于在距离家 \( A \) 公里和距离家 \( B \) 公里的两点之间来回走动。 \( \left| {A - B}\right| \) 是多少?
(A) \( \frac{2}{3} \) (B) 1 (C) \( 1\frac{1}{5} \) (D) \( 1\frac{1}{4} \) (E) \( 1\frac{1}{2} \)
解决方案 1
设亨利在两点之间行走,这两点为 \( P \) 和 \( Q \) ,其中 \( P \) 离家更近。根据题意,点 \( P \) 和 \( Q \) 到家的距离分别为 \( A \) 和 \( B \) 。由对称性,点 \( Q \) 到健身房的距离等于从家到点 \( P \) 的距离,因此 \( A = 2 - B \) 。此外,当他从点 \( Q \) 走向家时,他走了 \( \frac{3}{4} \) 的路程,最终停在点 \( P \) 。因此,我们知道 \( B - A = \frac{3}{4}B \) 。代入后得到
\[ B - A = \frac{3}{4}\left( {2 - A}\right) \text{. Adding these equations now gives} \]
\( 2\left( {B - A}\right) = \frac{3}{4}\left( {2 + B - A}\right) \) 乘以4,我们得到
\[ 8\left( {B - A}\right) = 6 + 3\left( {B - A}\right) \text{, so}B - A = \frac{6}{5} = \left( {\mathbf{C}2}\right) 1\frac{1}{5}\text{.} \]
解法2(不严谨)
我们假设亨利在点 \( P \) 和 \( Q \) 之间来回行走,且 \( P \) 比 \( Q \) 更靠近亨利的家。将亨利的家记为点 \( H \) ,健身房记为点 \( G \) 。于是 \( {HP} : {PQ} = 1 : 3 \) 且 \( {PQ} : {QG} = 3 : 1 \) ,因此 \( {HP} : {PQ} : {QG} = 1 : 3 : 1 \) 。
\[ \left| {A - B}\right| = {PQ} = \frac{3}{1 + 3 + 1} \cdot 2 = \frac{6}{5} = O\left( C\right) 1\frac{1}{5}. \]
解法3(不严谨;与解法2类似)
由于哈利几乎就在两点之间来回走动,我们把 \( A \) 记作更靠近他家的点, \( B \) 记作更靠近健身房的点。然后,我们把 \( A \) 到 \( B \) 的距离记作 \( x \) 。如果哈利在 \( B \) 并走了 \( \frac{3}{4} \) 的路程,他就会到达 \( A \) ,反之亦然。因此,我们可以说从 \( A \) 到健身房的距离是从 \( B \) 到他家距离的 \( \frac{1}{4} \) 倍。这意味着它是 \( \frac{1}{3}x \) 。这也适用于另一侧。此外,我们可以说 \( \frac{1}{3}x + x + \frac{1}{3}x = 2 \) 。我们解出 \( x \) 并得到 \( x = \frac{6}{5} \) 。因此,答案是(C) \( 1\frac{1}{5} \)
2019年AMC 10B试题/第19题
问题
设 \( S \) 为100,000的所有正整数约数(divisors)的集合。有多少个数可以表示为 \( S \) 中两个不同元素的乘积?
(A) 98 (B) 100 (C) 117 (D) 119 (E) 121
解决方案
100,000的质因数分解为 \( {2}^{5} \cdot {5}^{5} \) 。因此,我们选择两个数 \( {2}^{a}{5}^{b} \) 和 \( {2}^{c}{5}^{d} \) ,满足 \( 0 \leq a, b, c, d \leq 5 \) 和 \( \left( {a, b}\right) \neq \left( {c, d}\right) \) ,且它们的乘积为 \( {2}^{a + c}{5}^{b + d} \) ,其中 \( 0 \leq a + c \leq {10} \) 和 \( 0 \leq b + d \leq {10} \) 。
注意,这类似于选择 \( {100},{000}^{2} = {2}^{10}{5}^{10} \) 的一个因数,而 \( {100},{000}^{2} = {2}^{10}{5}^{10} \) 共有 \( \left( {{10} + 1}\right) \left( {{10} + 1}\right) = {121} \) 个因数。然而, \( {2}^{10}{5}^{10} \) 的某些因数无法表示为 \( {2}^{5} \cdot {5}^{5} \) 的两个不同因数的乘积,即: \( 1 = {2}^{0}{5}^{0} \) 、 \( {2}^{10}{5}^{10} \) 、 \( {2}^{10} \) 和 \( {5}^{10} \) 。最后两个无法如此表示,因为100,000中仅含2或仅含5的最大因数分别只有 \( {2}^{5} \) 或 \( {5}^{5} \) 。由于所选因数必须不同,最后两个数无法这样表示,因为它们需要 \( {2}^{5} \cdot {2}^{5} \) 或 \( {5}^{5} \cdot {5}^{5} \) 。前两个则分别需要 \( 1 \cdot 1 \) 和 \( {2}^{5}{5}^{5} \cdot {2}^{5}{5}^{5} \) 。这样共有 \( {121} - 4 = {117} \) 个候选数。不难证明,所有形如 \( {2}^{p}{5}^{q} \) 的数,其中 \( 0 \leq p, q \leq {10} \) ,且 \( p, q \) 不同时为0或10,都可以表示为 \( S \) 中两个不同元素的乘积。因此答案为 \( \left( \mathbf{C}\right) {117} \) 。
2019 AMC 10B 试题/第20题
以下题目同时出现在2019 AMC 10B第20题和2019 AMC 12B第15题,因此两道题均重定向至此页面。
题目
如图所示,线段 \( \overline{AD} \) 被点 \( B \) 和 \( C \) 三等分,使得 \( \underline{AB} = {BC} = {CD} = 2 \) 。三个半径为 \( 1,\widehat{\mathrm{{AEB}}},\widehat{\mathrm{{BFC}}} \) 的半圆
\( \overset{⏜}{\mathrm{{CGD}}} \) ,其直径位于 \( \overline{AD} \) 上,并分别在 \( E, F \) 和 \( G, \) 处与直线 \( {EG} \) 相切。一个半径为2的圆,其圆心位于 \( \bar{F} \) 。图中阴影区域(圆内但在三个半圆外的区域)的面积可表示为
\[ \frac{a}{b} \cdot \pi - \sqrt{c} + d \]
其中 \( a, b, c, \) 和 \( d \) 为正整数,且 \( a \) 与 \( b \) 互质。 \( a + b + c + d \) 是多少?
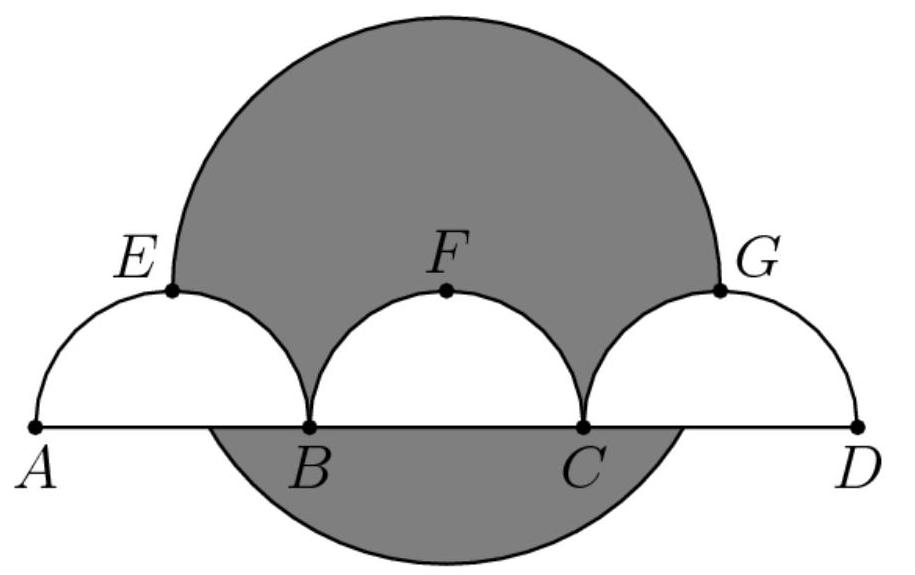
(A) 13 (B) 14 (C) 15 解答
将圆分为四部分:顶部半圆,通过连接E、F和 \( \operatorname{G}\left( A\right) \) ;底部扇形( \( B \) ),其弧角为 \( {120}^{ \circ } \) ,因为大圆半径为2,而短长度(较小半圆的半径)为1,从而得到
\( {30}^{ \circ } - {60}^{ \circ } - {90}^{ \circ } \) 三角形;由 \( A \) 的半径与弦 \( (C \) 构成的三角形;以及内切于正方形的圆(D)的四个角区域。于是面积为 \( A + B - C + D \) (在 \( B - C \) 中,我们求出底部阴影区域的面积,在 \( D \) 中,我们求出位于半圆之上但低于直径的阴影区域面积)。
\( A \) 的面积为 \( \frac{1}{2}\pi \cdot {2}^{2} = {2\pi } \) 。
\( B \) 的面积为 \( \frac{{120}^{ \circ }}{{360}^{ \circ }}\pi \cdot {2}^{2} = \frac{4\pi }{3} \) 。
对于 \( C \) 的面积,半径为2,距离为1(较小半圆的半径)到 \( {BC} \) ,形成两个 \( {30}^{ \circ } - {60}^{ \circ } - {90}^{ \circ } \) 三角形,因此 \( C \) 的面积为
\( 2 \cdot \frac{1}{2} \cdot 1 \cdot \sqrt{3} = \sqrt{3}. \)
\( D \) 的面积为 \( 4 \cdot 1 - \frac{1}{4}\pi \cdot {2}^{2} = 4 - \pi \) 。
因此,求出 \( A + B - C + D \) ,所求面积为 \( \frac{7\pi }{3} - \sqrt{3} + 4 \) ,所以
答案为 \( 7 + 3 + 3 + 4 = 6 \) 。(E) 17。
2019 AMC 10B 题目/第21题
题目
Debra反复抛掷一枚公平硬币,记录到目前为止出现的正面和反面总数,直到她连续出现两次正面或两次反面为止,此时停止抛掷。她最终连续出现两次正面,但在出现第二个正面之前先出现第二个反面的概率是多少?
(A) \( \frac{1}{36} \) (B) \( \frac{1}{24} \) (C) \( \frac{1}{18} \) (D) \( \frac{1}{12} \) (E) \( \frac{1}{6} \)
解法1
我们首先找出满足给定条件的抛掷序列。为了让Debra在出现第二个正面之前先看到第二个反面,她的第一次抛掷不能是正面,因为那样她要么在见到第二个正面之前就结束于两次反面,要么在见到两次反面之前就出现两次正面。因此,她的第一次抛掷必须是反面。她能够连续出现两次正面且在见到第二个正面之前先见到第二个反面的最短抛掷序列为 \( \overline{THTHH} \) ,其概率为 \( \frac{1}{{2}^{5}} = \frac{1}{32} \) 。此外,她可以通过额外添加一个 \( {TH} \) 来延长抛掷,其本身概率为 \( \frac{1}{{2}^{2}} = \frac{1}{4} \) 。由于她可以无限次这样做,这就得到一个无穷等比级数,因此答案(根据等比级数求和公式)为 \( \frac{\frac{1}{32}}{1 - \frac{1}{4}} = O\left( B\right) \frac{1}{24} \) 。解法2(更简便)
注意序列必须以THT开头,其概率为 \( \frac{1}{8} \) 。现在,设 \( P \) 为Debra在已抛掷THT后最终连续出现两次正面的概率。她要么立即连续出现两次正面(概率 \( \frac{1}{4} \) ),要么先出现一个正面再出现一个反面,回到“初始状态”(概率 \( \frac{1}{4}P \) )。因此, \( P = \frac{1}{4} + \frac{1}{4}P \) ,于是 \( P = \frac{1}{3} \) ,所以最终答案为 \( \frac{1}{8} \times \frac{1}{3} = O \) (B) \( \frac{1}{24} \) 。
2019 AMC 10B 题目/第22题
题目
拉尚(Raashan)、西尔维娅(Sylvia)和泰德(Ted)玩以下游戏。每人初始持有 \( \ $ 1 \) 。每15秒响一次铃,此时所有当前持有钱的玩家各自独立且随机地选择另外两人中的一人,并将 \( \mathfrak{\ $ }1 \) 交给该玩家。问:在铃声响过2019次后,每人恰好持有 \( \mathfrak{\ $ }1 \) 的概率是多少?(例如,拉尚和泰德可能都决定把 \( \mathfrak{\ $ }1 \) 给西尔维娅,而西尔维娅可能决定把自己的钱给泰德;此时拉尚将有 \( \ $ 0 \) ,西尔维娅将有 \( \ $ 2 \) ,泰德将有 \( \ $ 1 \) ,第一轮结束。第二轮中拉尚没有钱可给,但西尔维娅和泰德可能互相把 \( \ $ 1 \) 给对方,第二轮结束时持有量保持不变。)
(A) \( \frac{1}{7} \) (B) \( \frac{1}{4} \) (C) \( \frac{1}{3} \) (D) \( \frac{1}{2} \) (E) \( \frac{2}{3} \)
解法1
第一回合,每人初始持有 \( \ $ 1 \) 。此后每一回合只有两种可能:要么所有人仍保持 \( \ $ 1 \) ,我们记为(1-1-1);要么钱的分布以某种顺序变为 \( \mathfrak{\ $ }2 - \mathfrak{\ $ }1 - \mathfrak{\ $ }0 \) ,我们记为(2-1-0)。我们将分别考虑这两种状态。
在(1-1-1)状态下,每人有2种选择决定把钱给谁,因此共有 \( {2}^{3} = 8 \) 种可能的资金重排方式。注意,只有两种方式能使我们再次回到(1-1-1):
- 拉尚把钱给西尔维娅,西尔维娅把钱给特德,特德再把钱给拉尚。
- 拉尚把钱给特德,特德把钱给西尔维娅,西尔维娅再把钱给拉尚。
因此,停留在(1-1-1)状态的概率是 \( \frac{1}{4} \) ,而进入(2-1-0)状态的概率是 \( \frac{3}{4} \) (可以验证其余6种可能都导致(2-1-0))。
在(2-1-0)状态下,我们把拥有 \( \mathfrak{\ $ }2 \) 的人记为A,拥有 \( \mathfrak{\ $ }1 \) 的人记为B,拥有 \( \mathfrak{\ $ }0 \) 的人记为C。A有2种给钱对象可选,B也有2种给钱对象可选,因此共有 \( 2 \cdot 2 = 4 \) 种资金重新分配方式。只有当A把 \( \ $ 1 \) 给B,且B把 \( \ $ 1 \) 给C时,分配才会回到(1-1-1)。我们检查其余可能性,发现它们都回到
(2-1-0)。因此,进入(1-1-1)状态的概率是 \( \frac{1}{4} \) ,而
停留在(2-1-0)状态的概率是 \( \frac{3}{4} \) 。
无论处于哪种状态,进入(1-1-1)状态的概率始终是 \( \frac{1}{4} \) 。这意味着,在铃声响2018次之后,无论资金分配处于何种状态,第2019次铃响后进入(1-1-1)状态的概率都是 \( \frac{1}{4} \) 。因此,答案就是 \( \sigma \) (B) \( \frac{1}{4} \) 。
解法2(对称性)
第一次铃响后,要么一切不变,要么某人拥有 \( \ $ 2 \) 。不可能有人拥有 \( \ $ 3 \) ,因为在那假设的一轮中,那个人必须给出 \( \ $ 1 \) 。
因此,结果要么是 \( 1 - 1 - 1 \) ,要么是六种对称情形之一,其中一人得到 \( \mathfrak{\ $ }2 \) (例如 \( 1 - 2 - 0 \) 或 \( 2 - 1 - 0 \) 的分配)。三人交换美元回到同一 \( 1 - 1 - 1 \) 结果有两种方式。于是共有8
种总可能(这很合理,因为每人给出美元时有2种选择,共 \( {2}^{3} \) 种总可能)。因此,从 \( 1 - 1 - 1 \) 情形出发,回到 \( 1 - 1 - 1 \) 的概率是 \( 1/4 \) 。
不失一般性,取 \( 1 - 2 - 0 \) 情形。只有两人能出钱,铃响后共有 \( {2}^{2} \) 种可能结果。它要么分解回 \( 1 - 1 - 1 \) ,要么保持不变,要么变成 \( 0 - 1 - 2 \) ,要么变成 \( 0 - 2 - 1 \) 。因此,从 \( 1 - 1 - 1 \) 情形出发,回到 \( 1 - 1 - 1 \) 的概率是 \( 1/4 \) 。注意这对其余6种情形都成立。
由于初始状态有 \( 1/4 \) 概率保持不变,而其余6种对称状态各自也有 \( 1/4 \) 概率回到 \( 1 - 1 - 1 \) ,因此在任何状态后,最终为1-1-1的概率始终是1(B) \( \frac{1}{4} \)
2019 AMC 10B 试题/第23题
题目
点 \( A\left( {6,{13}}\right) \) 和 \( B\left( {{12},{11}}\right) \) 位于平面上的圆 \( \omega \) 上。假设圆 \( \omega \) 在 \( A \) 和 \( B \) 处的切线交于 \( x \) 轴上的一点,求圆 \( \omega \) 的面积。
(A) \( \frac{83\pi }{8} \) (B) \( \frac{21\pi }{2} \) (C) \( \frac{85\pi }{8} \) (D) \( \frac{43\pi }{4} \) (E) \( \frac{87\pi }{8} \)
解法1
首先,注意到两条切线长度相等。因此,设交点为(x,0),由勾股定理得
\[ \sqrt{{\left( x - 6\right) }^{2} + {13}^{2}} = \sqrt{{\left( x - {12}\right) }^{2} + {11}^{2}}\text{. This simplifies to}x = 5\text{.} \]
进一步,由于半径与切线成直角,四边形(风筝形)由圆心、 \( A \) 、 \( B \) 和(5,0)构成,且该四边形共圆。因此可应用托勒密定理得 \( 2\sqrt{170}x = d\sqrt{40} \) ,其中 \( x \) 为圆的半径, \( d \) 为圆心到(5,0)的距离。
因此, \( d = \sqrt{17}x \) 。对由点(5,0)、 \( A \) 或 \( B \) 之一以及圆心构成的三角形应用勾股定理,得 \( {170} + {x}^{2} = {17}{x}^{2} \) ,于是 \( {x}^{2} = \frac{85}{8} \) ,故答案为 \( \left| {\textbf{(C) }\frac{85}{8}\pi }\right| \) 。
解法2(坐标暴力法)
我们首先如解法1得到 \( x = 5 \) 。将点(5,0)记为 \( C \) 。线段 \( {AB} \) 的中点 \( M \) 为(9,12)。注意到圆心必在过 \( C \) 和 \( M \) 的直线上,因此圆心位于直线 \( y = {3x} - {15} \) 上。
直线 \( {AC} \) 为 \( y = {13x} - {65} \) 。因此与之垂直的直线斜率为 \( - \frac{1}{13} \) ,其方程为 \( y = - \frac{x}{13} + \frac{175}{13} \) 。
但注意到该直线必过 \( A\left( {6,{13}}\right) \) 和(x,3x-15)。于是 \( {3x} - {15} = - \frac{x}{13} + \frac{175}{13} \Rightarrow x = \frac{37}{4} \) 。因此圆心为 \( \left( {\frac{37}{4},\frac{51}{4}}\right) \) 。
最后,圆心 \( \left( {\frac{37}{4},\frac{51}{4}}\right) \) 与点 \( A \) 的距离为 \( \frac{\sqrt{170}}{4} \) 。于是
圆的面积为 \( \left( {c,\frac{85}{8}\pi }\right) \) 。
解法3
\( {AB} \) 的中点是 \( D\left( {9,{12}}\right) \) 。设在 \( A \) 和 \( B \) 处的切线交于 \( x \) 轴上的 \( C\left( {a,0}\right) \) ,则 \( {CD} \) 是 \( {AB} \) 的垂直平分线。设圆心为 \( O \) ,则 \( \bigtriangleup {AOC} \) 与 \( \bigtriangleup {DAC} \) 相似,故 \( \frac{OA}{AC} = \frac{AD}{DC} \) 。 \( {AB} \) 的斜率为 \( \frac{{13} - {11}}{6 - {12}} = \frac{-1}{3} \) ,因此 \( {CD} \) 的斜率为3,于是 \( {CD} \) 的方程为 \( y - 1\overline{2} = 3\left( {x - 9}\right) \Rightarrow y = {3x} - {15} \) 。令 \( y = 0 \) ,得 \( x = 5 \) ,故 \( C = \left( {5,0}\right) \) 。
现在我们计算 \( {AC} = \sqrt{{\left( 6 - 5\right) }^{2} + {\left( {13} - 0\right) }^{2}} = \sqrt{170} \) ,
\( {AD} = \sqrt{{\left( 6 - 9\right) }^{2} + {\left( {13} - {12}\right) }^{2}} = \sqrt{10} \) ,且
因此 \( {OA} = \frac{{AC} \cdot {AD}}{DC} = \sqrt{\frac{85}{8}} \) ,从而圆的面积
为 \( \pi \cdot O{A}^{2} = O\left( C\right) \frac{85}{8}\pi \) 。
解法4(你能多快计算两位数乘法?)
设(x,0)为x轴上的交点。由幂点定理, \( {\left( x - 6\right) }^{2} + {13}^{2} = {\left( x - {12}\right) }^{2} + {11}^{2} \Longrightarrow x = 5 \) 。于是过 \( A \) 和 \( B \) 的切线方程分别为 \( {13}\left( {x - 6}\right) + {13} = y \) 和 \( \frac{11}{7}\left( {x - {12}}\right) + {11} = y \) 。与它们垂直的直线为
\[ - \frac{1}{13}\left( {x - 6}\right) + {13} = y\text{and} - \frac{7}{11}\left( {x - {12}}\right) + {11} = y\text{. Thus,} \]
\[ - \frac{7}{11}\left( {x - {12}}\right) + {11} = - \frac{1}{13}\left( {x - 6}\right) + {13} \]
\[ \frac{{13} \cdot {7x} - {11x}}{{13} \cdot {11}} = \frac{{84} \cdot {13} - 6 \cdot {11} - 2 \cdot {11} \cdot {13}}{{11} \cdot {13}} \]
\[ {13} \cdot \left( \begin{aligned} {{7x} - 1} \\ 1 \end{aligned}\right) x = {84} \cdot {13} - 6 \cdot {11} - 2 \cdot {11} \cdot {13} \]
化简后, \( x = \frac{37}{4} \) 。于是 \( \omega \) 的圆心为 \( \left( {\frac{37}{4},\frac{51}{4}}\right) \) 。应用距离
公式。无妨设你使用 \( A \) ,则 \( \omega \) 的面积为
\[ \sqrt{\frac{{1}^{2}}{{4}^{2}} + \frac{{13}^{2}}{{4}^{2}}}\pi = \frac{170\pi }{16} \Rightarrow \left( {\mathbf{C})\frac{85}{8}\pi }\right) \]
- 由dolphin7进行小幅LaTeX编辑
解法5(幂点定理)
首先,根据幂点定理(power of a point theorem),两条切线的交点到点 \( A \) 和 \( B \) 的距离相等。这意味着我们可以轻松找到该点,即(5,0)。将此点标记为 \( X \) 。 \( \bigtriangleup {XAB} \) 是一个等腰三角形,边长分别为 \( \sqrt{170} \) 、 \( \sqrt{170} \) 和 \( 2\sqrt{10} \) 。将线段 \( {AB} \) 的中点标记为 \( M \) 。该三角形的高,即 \( \overline{XM} \) ,长度为 \( 4\sqrt{10} \) 。由于 \( \overline{XM} \) 平分 \( \overline{AB} \) , \( \overline{XM} \) 包含圆 \( \omega \) 的直径。设 \( \overset{⏜}{XM} \) 与圆 \( \omega \) 的两个交点为 \( P \) 和 \( Q \) ,其中 \( \overline{XP} \) 为较短者。现在令 \( \overline{MP} \) 为 \( x \) , \( \overline{MQ} \) 为 \( y \) 。根据 \( \overline{PQ} \) 和 \( \overline{AB} \) 的幂点定理, \( {xy} = {\left( \sqrt{10}\right) }^{2} = {10} \) 。再次对 \( \overline{XQ} \) 和 \( \overline{XA} \) 应用幂点定理, \( \left( {4\sqrt{10} - x}\right) \left( {4\sqrt{10} + y}\right) = {\left( \sqrt{170}\right) }^{2} = {170} \) 。利用 \( {xy} = {10} \) 这一事实进行展开, \( y = x + \frac{\sqrt{10}}{2} \) 。将其代入
。使用二次公式,
且由于。因为这是直径,
圆 \( \omega \) 的半径为 \( \frac{\sqrt{170}}{4} \) ,因此圆 \( \omega \) 的面积为
2019 AMC 10B 试题/第24题
题目
用递归方式定义一个数列: \( {x}_{0} = 5 \) 且
\[ {x}_{n + 1} = \frac{{x}_{n}^{2} + 5{x}_{n} + 4}{{x}_{n} + 6} \]
对所有非负整数 \( n \) 成立。设 \( m \) 是满足
\[ {x}_{m} \leq 4 + \frac{1}{{2}^{20}}. \]
的最小正整数,则 \( m \) 落在以下哪个区间内?
(A) \( \left\lbrack {9,{26}}\right\rbrack \) (B) \( \left\lbrack {{27},{80}}\right\rbrack \) (C) \( \left\lbrack {{81},{242}}\right\rbrack \) (D) \( \left\lbrack {{243},{728}}\right\rbrack \) (E) \( \left\lbrack {{729},\infty }\right\rbrack \)
解法1
我们首先用数学归纳法证明对所有 \( n \geq 0 \) , \( {x}_{n} > 4 \) 成立。观察到
\[ {x}_{n + 1} - 4 = \frac{{x}_{n}^{2} + 5{x}_{n} + 4 - 4\left( {{x}_{n} + 6}\right) }{{x}_{n} + 6} = \frac{\left( {{x}_{n} - 4}\right) \left( {{x}_{n} + 5}\right) }{{x}_{n} + 6} \]
因此(由于根据初始定义,对所有 \( n \) , \( {x}_{n} \) 显然为正),当且仅当 \( {x}_{n} > 4 \) 时, \( {x}_{n + 1} > 4 \) 成立。
类似地,我们证明 \( {x}_{n} \) 是递减的,因为
\[ {x}_{n + 1} - {x}_{n} = \frac{{x}_{n}^{2} + 5{x}_{n} + 4 - {x}_{n}\left( {{x}_{n} + 6}\right) }{{x}_{n} + 6} = \frac{4 - {x}_{n}}{{x}_{n} + 6} < 0 \]
现在我们需要估计 \( {x}_{n + 1} - 4 \) 的值,可通过重排后的方程
\[ {x}_{n + 1} - 4 = \left( {{x}_{n} - 4}\right) \cdot \frac{{x}_{n} + 5}{{x}_{n} + 6} \]
由于 \( {x}_{n} \) 递减, \( \frac{{x}_{n} + 5}{{x}_{n} + 6} \) 显然也递减,因此我们有
\[ \frac{9}{10} < \frac{{x}_{n} + 5}{{x}_{n} + 6} \leq \frac{10}{11} \]
且
\[ \frac{9}{10}\left( {{x}_{n} - 4}\right) < {x}_{n + 1} - 4 \leq \frac{10}{11}\left( {{x}_{n} - 4}\right) \]
这变为
\[ {\left( \frac{9}{10}\right) }^{n} = {\left( \frac{9}{10}\right) }^{n}\left( {{x}_{0} - 4}\right) < {x}_{n} - 4 \leq {\left( \frac{10}{11}\right) }^{n}\left( {{x}_{0} - 4}\right) = {\left( \frac{10}{11}\right) }^{n} \]
于是问题转化为求 \( n \) 的最小值,使得
\[ {\left( \frac{9}{10}\right) }^{n} < {x}_{n} - 4 \leq \frac{1}{{2}^{20}}\text{ and }{\left( \frac{10}{11}\right) }^{n - 1} > {x}_{n - 1} - 4 > \frac{1}{{2}^{20}} \]
取对数,我们得到 \( n\ln \frac{9}{10} < - {20}\ln 2 \) 和 \( \left( {n - 1}\right) \ln \frac{10}{11} > - {20}\ln 2 \) ,即
\[ n > \frac{{20}\ln 2}{\ln \frac{10}{9}}\text{ and }n - 1 < \frac{{20}\ln 2}{\ln \frac{11}{10}} \]
作为近似,我们可以使用 \( \ln \frac{10}{9} \approx \frac{1}{9} \) 、 \( \ln \frac{11}{10} \approx \frac{1}{10} \) 和 \( \ln 2 \approx {0.7} \) 。这些让我们估计出
\[ {126} < n < {141} \]
从而得到答案为 \( \left( {C,\left\lbrack {{81},{242}}\right\rbrack }\right) \)
解法2
当 \( {x}_{m} \leq 4 + \frac{1}{{2}^{20}} \) 的条件促使我们进行代换,将平衡点从4移到0。我们可以代换 \( {x}_{n} = {y}_{n} + 4 \) 来实现这一点。
现在,我们需要找到 \( m \) 的最小值,使得 \( {y}_{m} \leq \frac{1}{{2}^{20}} \) ,已知 \( {y}_{0} = 1 \) 且递推关系为
\[ {y}_{n + 1} = \frac{{y}_{n}^{2} + 9{y}_{n}}{{y}_{n} + {10}}. \]
凭借“一厢情愿”的思路,我们可以将递推关系简化如下:
\[ {y}_{n + 1} = \frac{{y}_{n}^{2} + 9{y}_{n} + {y}_{n} - {y}_{n}}{{y}_{n} + {10}} \]
\[ {y}_{n + 1} = \frac{{y}_{n}\left( {{y}_{n} + {10}}\right) - {y}_{n}}{{y}_{n} + {10}} \]
\[ {y}_{n + 1} = {y}_{n} - \frac{{y}_{n}}{{y}_{n} + {10}} \]
\[ {y}_{n + 1} = {y}_{n}\left( {1 - \frac{1}{{y}_{n} + {10}}}\right) \]
该递推关系看起来像一个几何序列,其公比在每一项后略微变化。从递推关系可见, \( {y}_{n} \) 序列严格递减,因此 \( {y}_{0} \) 之后的所有项都将小于1。同时,序列中的所有项均为正。这两点均可通过归纳法证明。
结合上述两点观察, \( \frac{9}{10} < 1 - \frac{1}{{y}_{n} + {10}} \leq \frac{10}{11} \) 。再考虑到递推关系类似于几何序列,我们得出 \( {\left( \frac{9}{10}\right) }^{n} < {y}_{n} \leq {\left( \frac{10}{11}\right) }^{n} \) 。
\( \frac{9}{10} \) 近似等于 \( \frac{10}{11} \) ,而答案选项给出的区间很宽松,因此我们应使用 \( \frac{9}{10} \) 或 \( \frac{10}{11} \) 来粗略估计 \( m.{\left( \frac{9}{10}\right) }^{3} \) 为0.729,而 \( \frac{1}{\sqrt{2}} \) 接近0.7,因为 \( {\left( {0.7}\right) }^{2} \) 为0.49,接近 \( \frac{1}{2} \) 。
因此,我们可以估计 \( {2}^{\frac{-1}{2}} < {y}_{3} \) 。
将两边同时取40次方,我们得到 \( {2}^{-{20}} < {\left( {y}_{3}\right) }^{40} \)
但 \( {y}_{3} = {\left( {y}_{0}\right) }^{3} \) ,所以 \( {2}^{-{20}} < {\left( {y}_{0}\right) }^{120} \) ,因此 \( {2}^{-{20}} < {y}_{120} \) 。
这告诉我们 \( m \) 大约在120左右,因此我们的答案是 \( \sigma \) (C) \( \left\lbrack {{81},{242}}\right\rbrack \)
解法3
由于选项给出的区间范围较宽,我们可以用近似法简化计算。注意到
\[ {x}_{n + 1} - {x}_{n} = \frac{4 - {x}_{n}}{{x}_{n} + 6} \]
并且 \( {x}_{0} = 5 \) ,我们知道 \( {x}_{n} \) 是一个递减序列,当接近4时下降速度减缓,且永远不会低于4。因此我们用4来近似 \( {x}_{n} \) 的分母,从而得到一个可解的差分方程:
\[ {x}_{n + 1} - {x}_{n} = \frac{4 - {x}_{n}}{10} \]
\[ {x}_{n + 1} = \frac{9}{10}{x}_{n} + \frac{2}{5} \]
用 \( {x}_{0} = 5 \) 求解,我们得到
\[ {x}_{n} = 4 + {\left( \frac{9}{10}\right) }^{n} \]
现在我们希望找到 \( n \) 使得
\[ {\left( \frac{9}{10}\right) }^{n} \approx \frac{1}{{2}^{20}} \]
\[ n \approx \frac{\log {2}^{20}}{\log {10} - \log 9} \approx \frac{{20} * {0.3}}{0.05} = {120} \]
由于120安全地落在[81,242]区间内,我们得到答案。 \( \mathrm{\left( C\right) \left\lbrack {{81},{242}}\right\rbrack } \)
2019 AMC 10B 第25题
以下题目同时出现在2019 AMC 10B第25题和2019 AMC 12B第23题,因此两道题均重定向至此页面。
题目
长度为19且仅由0和1组成的序列有多少个,满足:以0开头、以0结尾、不含连续两个0、不含连续三个1?
(A) 55 (B) 60 (C) 65 (D) 70 (E) 75 解法1(递推)
根据给定限制可推断,任何长度为 \( n \) 的有效序列必以0开头,随后接10或110。因此可定义递归函数 \( f\left( n\right) = f\left( {n - 3}\right) + f\left( {n - 2}\right) \) ,其中 \( f\left( n\right) \) 表示长度为 \( n \) 的有效序列数量。
这是因为对于任何长度为 \( n \) 的有效序列,在其后追加10或110,所得新序列仍满足所有条件。
容易手算出 \( f\left( 5\right) = 1 \) 的唯一可能序列为01010, \( f\left( 6\right) = 2 \) 的两种可能序列为 \( {011}\underline{0}{10} \) 和01010;再利用递推公式,我们得到 \( f\left( {19}\right) = \mathrm{\left( C\right) }{65} \) 。
解法2(分类讨论)
在任意一个特定0之后,序列中的下一个0必须恰好出现在向下2或3个位置处。在此情况下,我们从位置1开始,到位置19结束,即总共向下移动了18个位置。因此,我们必须将一系列2和3相加
以得到18。有多种方法可以做到这一点:
情况1:九个2——只有1种排列方式。
情况2:两个3和六个2——共有 \( \left( \begin{array}{l} 8 \\ 2 \end{array}\right) = {28} \) 种排列方式。
情况3:四个3和三个2——共有 \( \left( \begin{array}{l} 7 \\ 4 \end{array}\right) = {35} \) 种排列方式。
情况4:六个3——只有1种排列方式。